Từ hàng ngàn năm trước, con người đã bắt đầu quan sát chuyển động của các hành tinh và các ngôi sao và cho rằng Trái Đất là trung tâm vũ trụ. Đây là lý thuyết xuất phát từ nhà bác học người Hy Lạp Claudius Ptolemy (100 – 170 trước công nguyên). Lý thuyết này được chấp nhận trong suốt 1400 năm sau.
Mãi cho đến năm 1543, nhà bác học người Ba Lan Nicolaus Copernicus (1473 – 1543) mới đưa ra một nhận định là Trái Đất và các hành tinh khác quay quanh Mặt Trời. Sau đó, vì khao khát muốn tìm ra quy luật sắp xếp của bầu trời, nhà bác học người Đan Mạch Tycho Brahe (1546 – 1601) đã miệt mài quan sát sự chuyển động của các hành tinh và 777 ngôi sao mà mắt thường có thể nhìn thấy. Nhờ dữ liệu này mà người trợ lý của Brahe – Johannes Kepler đã bỏ ra 16 năm trời để tìm ra mô hình toán học giải thích chuyển động của các hành tinh.
Bạn đang xem: Các định luật Kepler và chuyển động của các hành tinh
Tuy nhiên, vì các dữ liệu này là do quan sát chuyển động ở tại Trái Đất nên gây ra rất nhiều khó khăn cho Kepler trong việc tính toán. Cuối cùng, Kepler cũng đã đưa ra được mô hình chính xác nhờ vào dữ liệu của Brahe về chuyển động của Sao Hỏa xung quanh Mặt Trời.
Lý thuyết của Kepler về chuyển động của các hành tinh được tóm tắt trong ba định luật:
1. Tất cả các hành tinh chuyển động theo các quỹ đạo elip trong đó Mặt Trời là một tiêu điểm.
2. Vecto bán kính kẻ từ Mặt Trời đến một hành tinh quét được những điện tích bằng nhau trong những khoảng thời gian bằng nhau.
3. Bình phương chu kỳ quỹ đạo của một hành tinh tỷ lệ với lập phương bán trục lớn của quỹ đạo elip của hành tinh đó.
Nội Dung
1. Định luật I Kepler: định luật về quỹ đạo
“Tất cả các hành tinh chuyển động theo các quỹ đạo elip trong đó Mặt Trời là một tiêu điểm.”
Các mô hình về hệ mặt trời lúc bấy giờ đều cho rằng quỹ đạo của các thiên thể đều là tròn. Tuy nhiên, theo định luật I Kepler, quỹ đạo tròn chỉ là một trường hợp đặc biệt, quỹ đạo elip mới là trường hợp tổng quát. Khám phá này của Kepler đã gặp rất nhiều thách thức vì phần lớn các nhà khoa học thời đó đều tin rằng quỹ đạo của các hành tinh có hình tròn hoàn hảo.
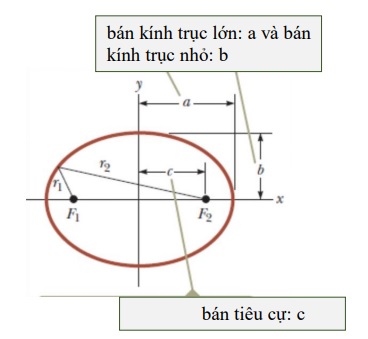
Như ta đã biết, một elip (hình 13.2) sẽ được đặc trưng bởi:
Xem thêm : Tác phẩm văn học là gì? Nội dung và hình thức của tác phẩm văn học
+ Bán kính trục lớn (a), kính trục nhỏ (b), bán tiêu cự (c), với:
a2 = b2 + c2
+ Độ lệch tâm: ? = ? ⁄ ? . Độ lệch tâm là tham số có giá trị từ 0 (đường tròn) đến nhỏ hơn 1 (khi độ lệch tâm tiến tới 1, elip tiến tới dạng parabol).
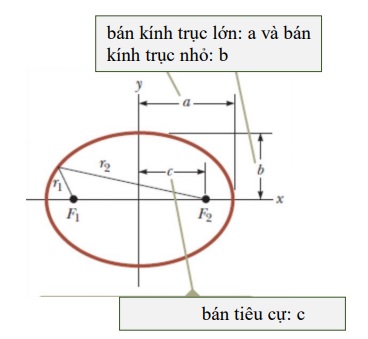
Dạng hình học quỹ đạo elip của các hành tinh
Độ lệch tâm quỹ đạo mà Kepler tính được cho Trái Đất là 0,017 vì vậy quỹ đạo của nó gần như là hình tròn. Đối với hành tinh có độ lệch tâm lớn nhất là Sao Thủy thì độ lệch tâm quỹ đạo của nó cũng chỉ là 0,21. Với các giá trị độ lệch tâm của các hành tinh thì quỹ đạo elip của các hành tinh rất khó phân biệt so với hình tròn. Chính vì lý do này mà các nghiên cứu của Kepler được đánh giá rất cao. Kể cả quỹ đạo elip của sao chổi Haley cũng được tính toán dựa trên định luật Kepler với độ lệch tâm là 0,97. Với bán kính trục lớn rất dài so với bán kính trục nhỏ, sao chổi Haley phải mất đến 76 năm mới chuyển động hết một vòng xung quanh Mặt Trời.
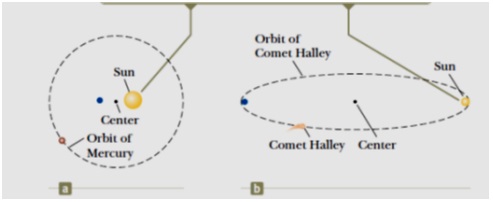
Quỹ đạo của sao Thủy (hình a) và quỹ đạo của sao chổi Haley (hình b)
Định luật I Kepler là kết quả trực tiếp của tính chất tỷ lệ nghịch với bình phương khoảng cách của lực hấp dẫn. Dưới tác dụng của lực hấp dẫn gây ra bởi Mặt trời, các thiên thể có thể chuyển động theo các quỹ đạo hình elip (các hành tinh, tiểu hành tinh, sao chổi) hoặc parabol hoặc hyperbol (thiên thạch).
2. Định luật II Kepler: định luật về tốc độ diện tích
“Vecto bán kính kẻ từ Mặt Trời đến một hành tinh quét được những điện tích bằng nhau trong những khoảng thời gian bằng nhau.”
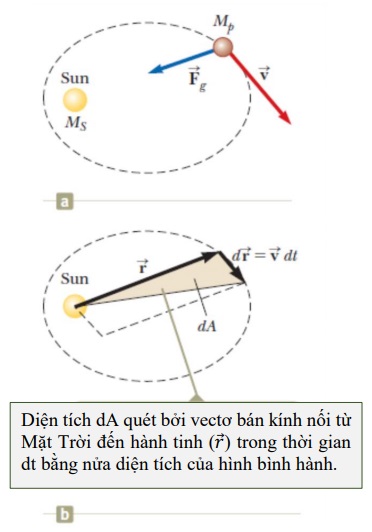
– Hình a: tác dụng lực hút của Mặt Trời lên hành tinh
– Hình b: trong thời gian dt, hình bình hành được tạo nên bởi 2 vectơ bán kính ? (với gốc tọa độ đặt ở Mặt Trời)
Moment quỹ đạo ?⃗ của chuyển động của các hành tinh là một hằng số:
Moment của lực hấp dẫn mà Mặt Trời tác dụng lên hành tinh đối với trục qua Mặt trời bằng không nên moment động lượng của hành tinh đối với trục qua Mặt trời được bảo toàn:
3. Định luật III Kepler: định luật về chu kỳ
“Bình phương chu kỳ quỹ đạo của một hành tinh tỷ lệ với lập phương bán trục lớn của quỹ đạo elip của hành tinh đó”
Định luật này có thể được dẫn ra cho một hành tinh có quỹ đạo tròn như sau:
Theo định luật II Newton, dưới tác dụng lực hấp dẫn Fg của Mặt Trời, hành tinh có khối lượng Mp đang khảo sát sẽ có gia tốc a:
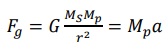
Với ? là gia tốc chuyển động tròn của hành tinh:
• v: vận tốc của hành tinh, r là bán kính quỹ đạo tròn của hành tinh quanh Mặt Trời.
• Fg là lực hấp dẫn của Mặt Trời tác dụng lên hành tinh đang khảo sát
• MS là khối lượng của Mặt Trời
• Mp là khối lượng của hành tinh đang khảo sát
Từ 2 công thức trên ta có:
Nguồn: https://25giay.vn
Danh mục: Tin Tức
