Số thực là gì (r là tập số gì), định nghĩa & tính chất số thực

Trong bài viết này chúng tôi sẽ cùng các bạn tìm hiểu về số thực là gì. Những khái niệm cơ bản về số thực, các tính chất cũng như những ví dụ minh họa để các bạn hiểu rõ hơn vai trò của số thực trong Toán học như thế nào.

Những kiến thức cần nhớ về số thực

Số thực là gì?

Theo Wikipedia thì một số thực bao gồm tất cả các số hữu tỉ, chẳng hạn như số nguyên −5 và phần số 4/3 và tất cả các số vô tỉ, chẳng hạn như √ 2 (1.41421356…, căn bậc hai của 2, số đại số vô tỉ).

Bạn đang xem: Số thực là gì (r là tập số gì), định nghĩa & tính chất số thực

Hoặc một cách dễ hiểu hơn là số thích chính là tập hợp bao gồm số dương (như 1, 2, 3), số 0, số âm (-1,- 2, -3), số hữu tỉ, số vô tỉ. Tức có nghĩa số thực gồm có thể được xem là các điểm nằm trên trục số dài vô hạn. Ngắn gọn hơn thì số thực là tập hợp các số hữu tỉ và số vô tỉ.

Tính chất của số thức

• Bất kỳ số thực khác không là số âm hoặc số dương.
• Tổng hay tích của hai số thực không âm là một số thực không âm.
• Số thực là tập hợp vô hạn các số vô cùng nhiều không đếm được các số thực.
• Có hệ thống các tập hợp con vô hạn có thể đếm được của các số thực.
• Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục
• Số thực có thể biểu thị bằng biểu diễn thập phân.

Định nghĩa về tập hợp R

R là gì?

R trong toán học là gì? Câu trả lời: R chính là kí hiệu của số thực bao gồm số hữu tỉ và số vô tỉ.

Ta có: Tập hợp số thực kí hiệu là R (R=Q U I)

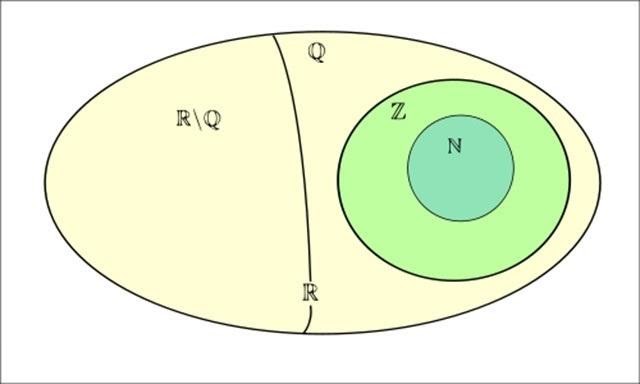
Tập hợp của các số thực được biểu diễn qua hình vẽ sau đây:

Trong đó:

Xem thêm : Figured Out là gì và cấu trúc cụm từ Figured Out trong câu Tiếng Anh

N: Tập hợp số tự nhiên

Z: Tập hợp số nguyên

Q: Tập hợp số hữu tỉ

I = RQ: Tập hợp số vô tỉ

Vậy R là tập hợp số thực

Trục số thực

Mối số thực được biểu diễn bởi một điểm trên trục số. Và ngược lại, tức mỗi điểm trên trục số sẽ biểu diễn một số thực. Chỉ có tập hợp số thực mới có thể lấp đầy trục số.

Trong tập hợp R, ta cũng định nghĩa các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc…Và trong các phép toán các số thực cũng có các tính chất như các phép toán trong tập hợp các số hữu tỉ.

Xem thêm : Dải ngân hà là gì?

Ta có: N ⊂ Z ⊂ Q ⊂ R.

Các thuộc tính của số thực

Ký hiệu R trong toán học được hiểu là số thực và chúng có các thuộc tính là:

• Chúng cho biết các số thực bao gồm một trường, với phép cộng và phép nhân cùng với phép chia cho các số khác 0. Chúng có thể sắp xếp trên một trục số hoành theo cách tương thích với phép cộng và phép nhân.
• Chúng cho biết nếu tập hợp một số thực không trống có giới hạn trên thì nó có cận trên chính là những số thực nhỏ nhất.

Ví dụ dễ hiểu về số thực trong toán học

Tập hợp R là ký hiệu của tập hợp số thực, gồm số hữu tỉ và số vô tỉ:

Chẳng hạn như số nguyên là: −5, 2, 3, -8…

Phân Số là: 4/3, 8/5,..

Số Vô Tỷ như: √ 2 (1.41421356…); 3,1456;…

Nhiều người thắc mắc về 0 có phải là số nguyên không? Câu trả lời là có, bởi số nguyên là tập hợp bao gồm các số không (0), số tự nhiên dương và các số đối của chúng còn gọi là số tự nhiên âm. Tập hợp số nguyên là vô hạn nhưng có thể đếm được và kí hiệu là Z.

Kết luận

Vậy khi một ai đó hỏi bạn số thực là gì, R là gì hay R là tập hợp số gì? Thì với những kiến thức trong bài viết này sẽ giúp bạn trả lời chính xác các câu hỏi đó. Hi vọng các bạn sẽ nắm rõ các kiến thức về tập hợp r là gì trong toán học để có thể áp dụng giải các bài tập được nhanh gọn và dễ dàng hơn.

Nguồn: https://25giay.vn
Danh mục: Hỏi Đáp