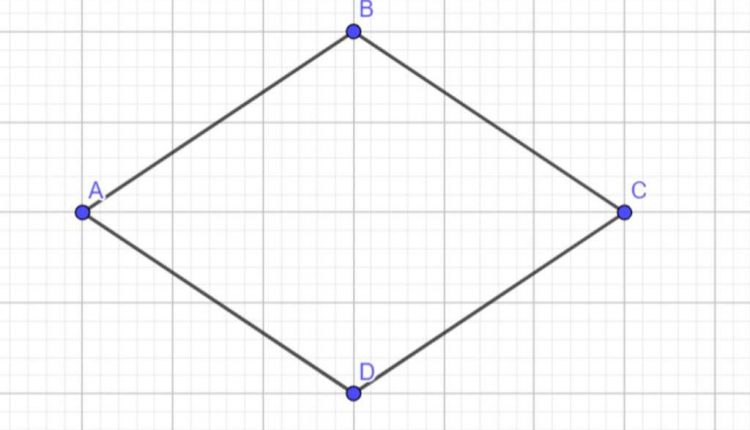
Cách vẽ hình thoi đơn giản + Lý thuyết, bài tập đầy đủ
Bên cạnh hình vuông, hình chữ nhật thì hình thoi cũng là một phần quan trọng của chương trình Toán THCS. Dưới đây sẽ là cách vẽ hình thoi, đặc điểm, tính chất,… đầy đủ, chi tiết nhất giúp bạn giải các bài tập dễ dàng hơn nhé.
Nội Dung
Khái niệm hình thoi & ứng dụng trong cuộc sống
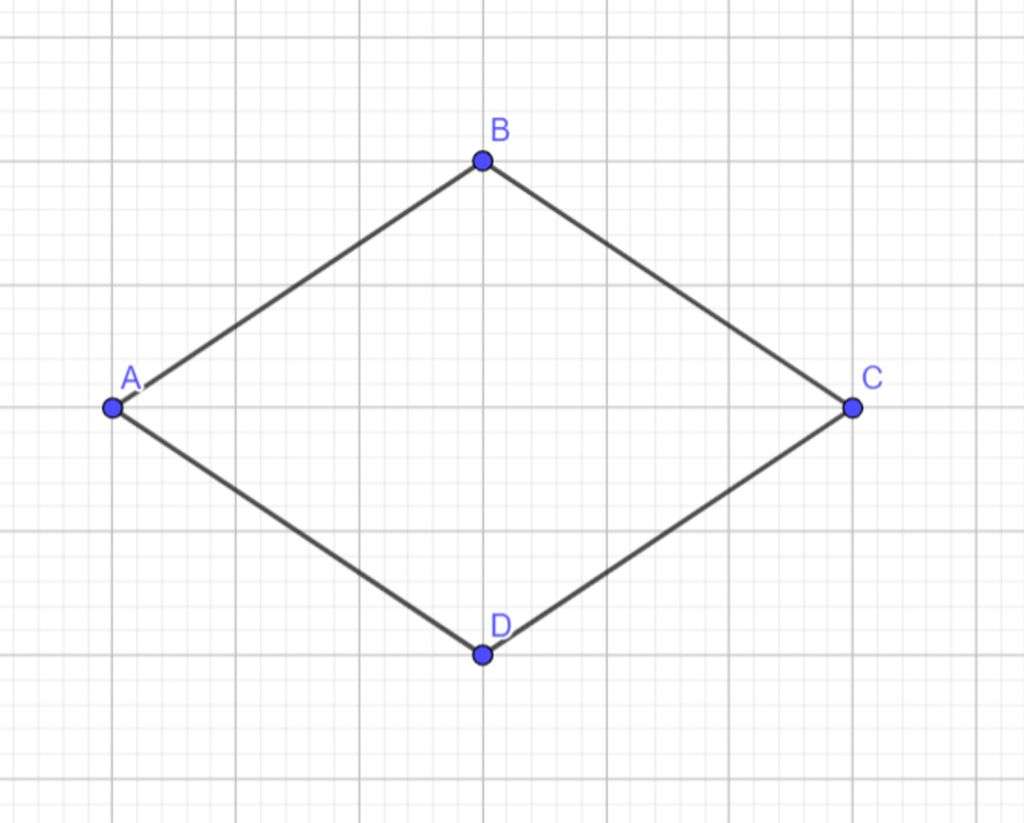
Theo như trong hình học Ơ-clit, hình thoi là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.
Tuy có cấu trúc đơn giản nhưng hình thoi lại được ứng dụng trong nhiều lĩnh vực khác nhau, cụ thể:
– Lĩnh vực vật lý và kỹ thuật: Hình thoi thường xuất hiện trong các bản vẽ kỹ thuật, nhất là trong việc biểu diễn các cấu trúc đối xứng và cơ cấu.
– Lĩnh vực Toán học và hình học: Hình thoi là một phần quan trọng của hình học và toán học cơ bản. Nó thường được sử dụng để minh họa các khái niệm về tỷ lệ, đối xứng và các tính chất hình học cơ bản.
– Lĩnh vực kỹ thuật cơ điện tử: Hình thoi được sử dụng trong thiết kế các bánh răng và các bộ phận máy móc khác để chuyển động hoặc truyền động.
– Lĩnh vực trang sức & thiết kế: Hình thoi thường được sử dụng trong thiết kế trang sức, ví dụ như nhẫn và mặt đá quý, để tạo ra các thiết kế đẹp và độc đáo.
– Lĩnh vực thiết kế đồ họa: Hình thoi được sử dụng trong thiết kế đồ họa và đồ họa máy tính để tạo ra các biểu đồ và biểu đồ đơn giản. Hoặc tạo ra các hình dáng độc đáo hơn.
– Lĩnh vực khoan và cắt kim loại: Hình thoi được sử dụng trong quá trình khoan và cắt kim loại để tạo ra các lỗ hoặc mặt tiếp xúc đặc biệt.

Phân loại các dạng hình thoi hiện nay
Không chỉ có một hình dạng duy nhất, hình thoi được phân loại dựa trên các đặc điểm khác nhau như kích thước hay góc. Dưới đây sẽ là một số phân loại chính để bạn hiểu rõ hơn nhé.
| CÁC LOẠI HÌNH THOI | ĐẶC ĐIỂM CHÍNH |
| Hình thoi lớn và nhỏ | – Hình thoi này được phân thành hai loại chính dựa trên kích thước của nó. – Hình thoi nhỏ có các cạnh và đường chéo ngắn hơn so với hình thoi lớn. |
| Hình thoi cân và không cân | – Hình thoi cân là loại hình thoi có các góc và cạnh bằng nhau. – Hình thoi không cân có các cạnh và góc không bằng nhau. |
| Hình thoi đều và không đều | – Hình thoi đều là loại hình thoi mà cả bốn cạnh và hai đường chéo đều có độ dài bằng nhau. – Hình thoi không đều, tuy nó vẫn là một hình thoi, có các cạnh và đường chéo có độ dài không bằng nhau. |
| Hình thoi vuông và không vuông | – Hình thoi vuông là một loại hình thoi có bốn góc vuông, tức là các góc trong nó có độ lớn là 90 độ. – Hình thoi không vuông có các góc không phải là góc vuông. |
| Hình thoi bình thường và biến thể | – Hình thoi bình thường là một hình thoi cơ bản với các đặc điểm tiêu chuẩn. – Hình thoi biến thể là các loại hình thoi có sự biến đổi hoặc thay đổi đối với các đặc điểm tiêu chuẩn, chẳng hạn như hình thoi nghiêng. |
Những tính chất đặc trưng của hình thoi
Trước khi bắt tay vào học cách vẽ hình thoi, bạn cần biết đặc trưng của chúng. Như vậy khi thực hành sẽ dễ dàng hơn.
| TÍNH CHẤT ĐẶC TRƯNG | CỤ THỂ HƠN |
| Các cạnh có độ dài bằng nhau | Các cạnh của hình thoi đều có độ dài bằng nhau. Điều này tạo ra sự đối xứng trong hình dáng của nó. |
| Các góc có độ lớn bằng nhau | Các góc trong hình thoi cũng có độ lớn bằng nhau. Thường thì các góc này đều có độ lớn là 60 độ, tạo thành một hình góc vuông đều bên trong hình thoi. |
| Điểm đối xứng | Hình thoi có điểm đối xứng, tức là một đường thẳng đi qua tâm của nó có thể chia hình thoi thành hai phần đối xứng nhau. |
| Đường chéo có tính chất đặc biệt | Hình thoi có hai đường chéo, mỗi đường nối hai đỉnh không liên tiếp của nó. Điều đặc biệt là, các đường chéo cắt nhau vuông góc tại tâm của hình thoi, chia hình thoi thành bốn tam giác đều có cùng độ lớn. |
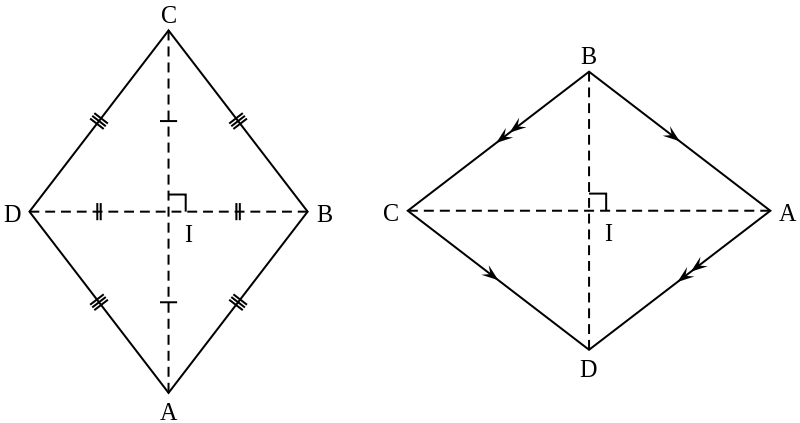
Những dấu hiệu nhận biết hình thoi
Dựa vào tính chất của hình thoi ở trên, bạn có thể nhận biết hình thoi khi phân biệt với một số hình học khác. Điều này sẽ giúp ích khi đề toán yêu cầu bạn phải chứng minh đó là hình thoi.
– Hình tứ giác đặc biệt
- Tứ giác có bốn cạnh bằng nhau là hình thoi
- Tứ giác có hai đường chéo là đường trung trực của nhau là hình thoi
- Tứ giác có hai đường chéo là đường phân giác của cả bốn góc là hình thoi.
– Hình bình hành đặc biệt
- Hình bình hành có hai cạnh kề bằng nhau là hình thoi
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
- Hình bình hành có hai đường chéo là đường phân giác của một góc là hình thoi
Cách 1 : Cách vẽ hình thoi bằng thước kẻ và êke
– Bước 1: Trước tiên, bạn vẽ một đoạn thẳng AC với độ dài bất kỳ hoặc cho trước. Sau đó tiến hành xác định trung điểm O của đoạn thẳng AC.
– Bước 2: Bạn dùng êke vẽ đoạn thẳng BD vuông góc với AC tại O và nhận O là trung điểm của BD.
– Bước 3: Tiếp đến bạn nối các đỉnh A với B, B với C, C với D, D với A. Như vậy là được hình thoi ABCD rồi nhé.
Cách 2: Cách vẽ hình thoi bằng thước kẻ & compa
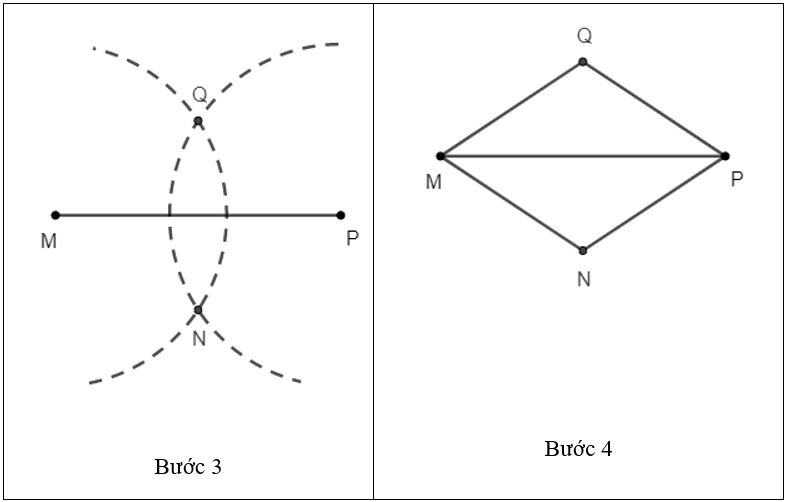
– Bước 1: Trước tiên, bạn dùng thước vẽ đoạn thẳng AC có độ dài bất kỳ.
– Bước 2: Sau đó, bạn dùng compa để vẽ đường tròn tâm A bán kính bất kỳ. Gọi E, F lần lượt là các điểm giao của đường tròn với đoạn thẳng AC (E nằm giữa A và F).
– Bước 3: Tiếp đến, bạn dùng compa vẽ đường tròn tâm E bán kính bằng độ dài đoạn EF. Đường tròn cắt AB và BC lần lượt tại các điểm G, H.
– Bước 4: Bạn dùng thước vẽ đoạn thẳng GH. Đường thẳng GH chính là đường chéo của hình thoi ABCD cần vẽ.
– Bước 5: Sau đó dùng thước để vẽ đoạn thẳng vuông góc với đường chéo GH tại điểm giao của nó với đường thẳng AB (gọi điểm đó là I). Kéo dài đoạn thẳng IH để nó cắt đường chéo GH tại điểm J.
– Bước 6: Giờ bạn chỉ cần nối các điểm A, I, J, và D với nhau sẽ được hình thoi ABCD.
Xem thêm : Phát hành chứng khoán là gì? Mục đích và các phương thức phát hành
Lưu ý: Các độ dài và góc vẽ có thể tuỳ ý chọn, miễn sao các bước vẽ đúng theo trình tự trên.
Ví dụ cách vẽ hình thoi
– Đề bài: Hãy dùng thước và compa vẽ hình thoi ABCD, biết AB = 5cm và AC = 8cm.
– Lời giải: Để vẽ hình thoi ABCD, ta thực hiện theo các bước dưới đây:
- Bước 1: Trước tiên, dùng thước vẽ đoạn thẳng AC = 8 cm.
- Bước 2: Sau đó dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm.
- Bước 3: Tiếp đến dùng compa vẽ một phần đường tròn tâm C bán kính 5 cm; phần đường tròn này cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm B và D.
- Bước 4: Cuối cùng, dùng thước vẽ các đoạn thẳng AB, BC, CD, DA là được hình thoi ABCD.
Công thức tính chu vi hình thoi
Công thức tính chu vi hình thoi cũng rất quan trọng. Trên lý thuyết, chu vi của hình thoi được tính bằng tổng độ dài các đường bao quanh hình cũng chính bằng độ dài một cạnh nhân với 4.
P = a x 4
Trong đó: P là chu vi hình thoi. a là cạnh hình thoi
Công thức tính diện tích hình thoi
Diện tích của hình thoi là diện tích được đo bằng độ lớn của bề mặt hình, là phần mặt phẳng ta có thể nhìn thấy của hình thoi và được tính bằng nửa tích độ dài của hai đường chéo.
S = ½ x d1 x d2 hoặc = h x a
Trong đó: S là diện tích hình thoi
d1, d2 là hai đường chéo hình thoi
h là chiều cao của hình thoi
a là cạnh hình thoi
Bài tập liên quan đến hình thoi
Ví dụ 1: Nhận biết hình thoi? Và giải thích tại sao?
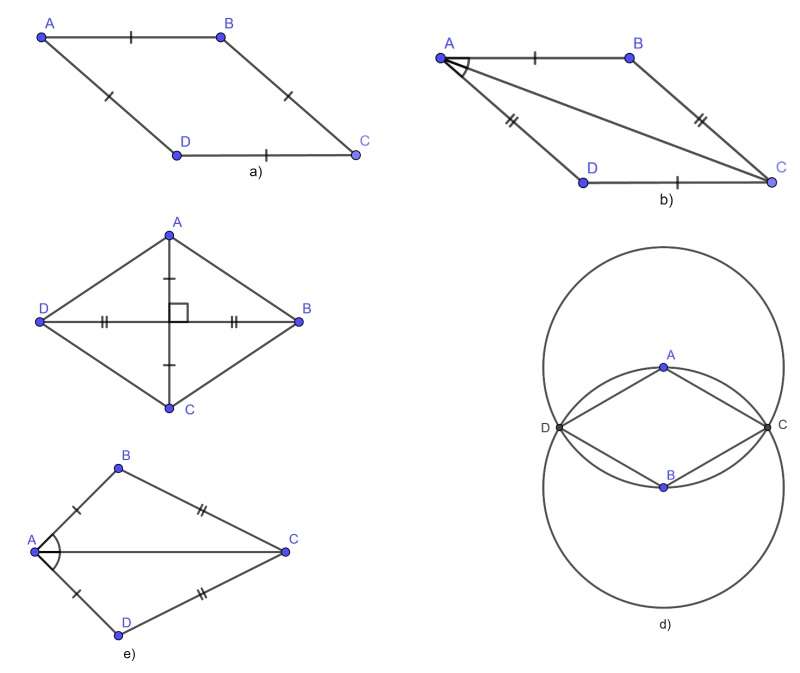
Hướng dẫn:
– a) Tứ giác ABCD có AB = BC = CD = DA nên ABCD là hình thoi
– b) Tứ giác ABCD có AB = CD, AD = BC nên ABCD là hình bình hành. Hình bình hành ABCD có đường chéo AC là đường phân giác góc A nên ABCD là hình thoi.
– c) Tứ giác ABCD với hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường nên ABCD là hình thoi
– d) Ta có: B, C, D đều thuộc đường tròn tâm A nên AB = AC = AD (1)
- A, C, D đều thuộc đường tròn tâm B nên AB = BC = BD (2)
- Từ (1) và (2) suy ra, AC = AD = BC = BD
- Do đó, ABCD là hình thoi.
– e) Tứ giác ABCD có các cạnh đối diện không bằng nhau, do đó ABCD không là hình thoi.
Ví dụ 2: Tính chu vi của hình thoi ABCD có độ dài cạnh bằng 4 cm
Hướng dẫn
Chu vi hình thoi ABCD = AB x 4 = 4 x 4 = 16 cm
Ví dụ 3: Cho hình thoi ABCD có AB = BC = CD = DA = 5cm. Tính diện tích hình thoi.
Hướng dẫn:
Áp dụng công thức ta có chu vi hình thoi ABCD là:
P = 4.5 = 20(cm)
Ví dụ 4: Cho tứ giác ABCD có AC = BD. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh tứ giác EFGH là hình thoi.
Lời giải
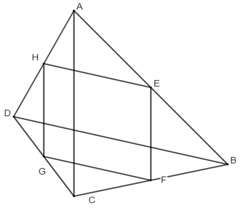
Vì E là trung điểm của AB, F là trung điểm của BC nên EF là đường trung bình của tam giác ABC
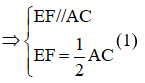
Vì G là trung điểm của DC, H là trung điểm của DA nên HG là đường trung bình của tam giác ADC
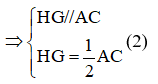
Từ (1) và (2) =>
=> Tứ giác EFGH là hình bình hành.
Lại có G là trung điểm của DC, F là trung điểm của BC nên GF là đường trung bình của tam giác BCD.
![]()
Mà BD = AC
Nên GF = EF
Hình bình hành có hai cạnh kề bằng nhau là hình thoi nên tứ giác EFGH là hình thoi.
Ví dụ 5: Cho hình thang ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AB, CD, BD, AC.
a) Chứng minh tứ giác MPNQ là hình bình hành;
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi?
Lời giải:
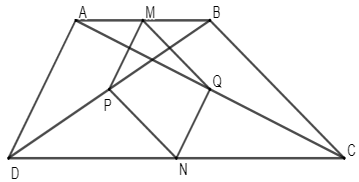
a) Vì M là trung điểm của AB, P là trung điểm của BD nên MP là đường trung bình của tam giác ABD
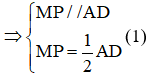
Vì Q là trung điểm của AC, N là trung điểm của DC nên QN là đường trung bình của tam giác ACD
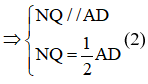
Từ (1) và (2)
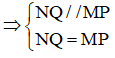
Xét tứ giác MPNQ có:
NQ // MP
NQ = MP
Do đó: tứ giác MPNQ là hình bình hành.
b) Để hình bình hành MPNQ là hình thoi thì MP = MQ
Vì M là trung điểm của AB, Q là trung điểm của AC nên MQ là đường trung bình của tam giác ABC
![]()
Để MQ = MP thì
![]()
Vậy để MPNQ là hình thoi thì hình thang ABCD phải có hai cạnh bên AD và BC bằng nhau.
Như vậy, bạn đã biết cách vẽ hình thoi đơn giản với các dụng cụ quen thuộc. Hi vọng những thông tin trên sẽ giúp mọi người giải Toán nhanh hơn nhé.
Nguồn: https://25giay.vn
Danh mục: Tin Tức